近日， 我校大数据科学与产业研究院DIG（Data Intelligence Generation）团队在人工智能领域国际顶尖期刊《IEEE Transactions on Pattern Analysis and Machine Intelligence》（IEEE TPAMI， 影响因子：24.314）在线刊发了题为《Generalization Performance of Pure Accuracy and Its Application in Selective Ensemble Learning》的研究论文。青年教师王婕婷为第一作者，钱宇华教授为通讯作者，青年教师李飞江与梁吉业教授、香港城市大学张青富教授为合作者。

本研究通过构建可消除随机一致性的一致性度量范式，导出纯准确度度量，通过理论和实验得出了其相对于准确度指标的三大优势：类别分布不敏感性、低偏差性和高辨识性（如图1所示）。 这些性质为基于纯准确度的可学习理论与方法提供了理论支撑。

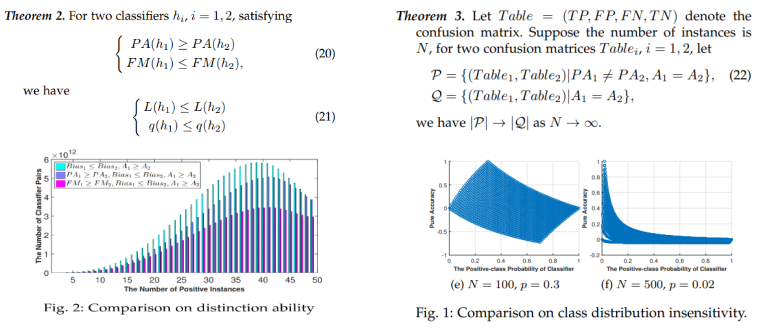
图1 纯准确度的类别分布不敏感性、低偏差性和高辨识性

学习能力考察学习模型在未知数据上的泛化能力，理论内涵是探索真实风险与经验风险之间差距上界的收敛因子和收敛速度，从而评估学习模型的推广能力。更紧的差距上界不仅有助于更精确地估计模型达到指定泛化能力所需的样本量，还可指导设计泛化能力更强的学习原则与学习算法。为了给出纯准确度的更紧的上界，文章首先证明可加性函数的离差上确界是自界的，使得自界性诱导的次泊松不等式适用于改善可加性函数的泛化上界。 接着， 证明了次泊松不等式的置信度函数是不可逆的，这导致从概率上界到泛化误差上界的推导不可行。本研究给出了一个更紧的基本不等式放大次泊松不等式，使其可用于上界的表示。基于上述基本理论，给出可加性函数、准确度和纯准确度更紧的泛化界（如图2所示）。

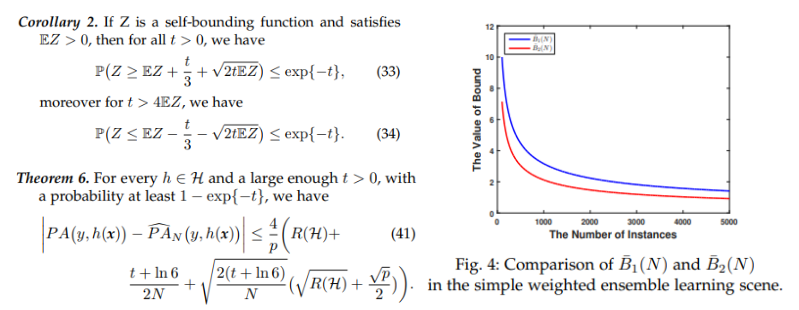
图2 更紧的概率不等式与泛化误差上界

本研究将进一步提出的随机一致性可学习理论用于集成学习类方法的重构，提出了优化纯准确度的选择性集成模型PASE，并通过分式规划和一维全局最优搜索方法求解模型，基准测试集和图像数据集表明，PASE比现有的基于准确度的选择性集成方法更有效（如图3所示）。 与现有可以优化纯准确度的方法相比，PASE能够更好地优化PA值。通过高维图像数据集，验证了PASE适用于提升弱分类器（如图4所示）。

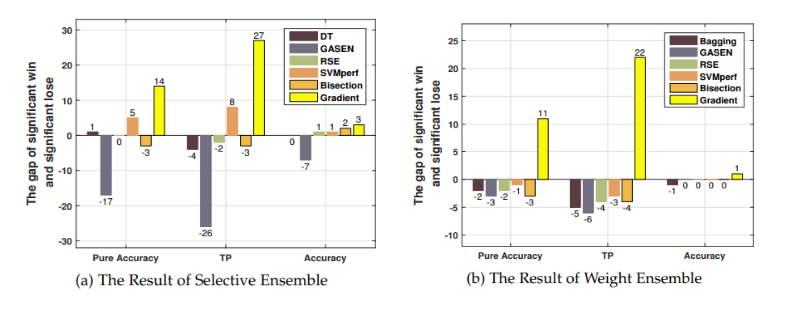
图3 基于纯准确度的选择性集成算法与基准算法对比

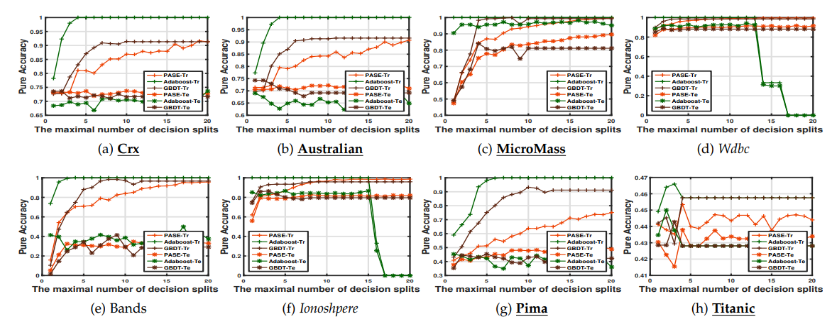
图4 基于纯准确度的选择性集成算法与提升算法对比

研究工作得到计算智能与中文信息处理教育部重点实验室、山西省机器视觉与数据挖掘工程研究中心、国家自然科学基金重点基金、国家重点研发计划、国家自然科学基金青年基金、山西省三晋学者人才计划的支持。

研究成果原文链接：https://ieeexplore.ieee.org/document/9765714